感知机学习算法
本文最后更新于:2022年6月28日星期二晚上10点39分
实验原理
感知机学习算法
原始形式
- 感知机模型:$f(x)=sign(\omega x + \theta)$
- 输入:训练集
- $T={(x_1, y_1),(x_2,y_2,…,(x_n, y_n))}$
- $x_i\in X=R^n$
- $y_i\in{1,-1}$
- $i=1,2,…,n$
- 学习率 $\eta$:$0< \eta \leq 1$
- $T={(x_1, y_1),(x_2,y_2,…,(x_n, y_n))}$
- 输出:$\omega$,$\theta$
- 步骤:
- 选定初值 $\omega_0, \theta_0$
一般都是 0
- 从训练集中选出数据 $(x_i,y_i)$
- 当 $y_i(\omega x_i + \theta) \leq 0$ 时,更新 $\omega, \theta$:
- $\omega \leftarrow \omega + \eta x_iy_i$
- $\theta \leftarrow \theta + \eta y_i$
- 继续执行第二步,直至训练集中没有误分类点
- 选定初值 $\omega_0, \theta_0$
数据集介绍
/感知机数据集/perceptron_data.txt共有 98 个样本 2 个输入变量
数据格式如下图:
实验环境
Python版本:Python 3.9- 编辑器:
Jupyter Notebook、PyCharm - 扩展包:
numpy、pandas、matplotlib等基础扩展包不可使用
sklearn、kreas等机器学习包
实验要求
- 采用感知机学习算法建立模型
- 神经元激活函数建议选用
sign函数(数据集最后一列的标签请将
0转换为-1) - 迭代输出每一次更新后的 $\omega$ 和 $\theta$
- 数据集线性可分,最好求解出线性超平面
实验代码详解
感知机
根据上述的感知机学习算法编写代码:
def perceptron(data_x, data_y, eta):
"""
感知机学习算法
:param data_x: 样本
:param data_y: 标签
:param eta: 学习率
:return: w, θ
"""
omega = np.zeros(data_x.shape[1])
theta = 0
classify_count = 0 # 记录分类次数
classify_round = 0 # 记录分类轮次
classify_right = False # 记录误分类点的存在
new_round = True
while not classify_right:
if new_round:
print("第 %d 轮:" % classify_round)
classify_round += 1
classify_right = True
new_round = False
for index in range(0, data_x.shape[0]):
if data_y[index] * (np.dot(omega, data_x[index]) + theta) <= 0:
theta += eta * data_y[index]
omega += eta * data_x[index] * data_y[index]
classify_count += 1
print("分类次数:%d\t θ: %.2f\t w:" % (classify_count, theta), omega)
# 绘图
table_line(data_x[:, 0], data_x[:, 1], data_y, omega, theta, classify_count)
classify_right = False
new_round = True
return omega, theta绘图
绘图主要是两个部分:
- 训练集根据 [0, 1] 划分后的散点图
- 随着 $\omega, \theta$ 的变化而变化的含有超平面的图
def get_scatter_data(x_axis, y_axis, label):
"""
对数据按照 label【0,1】进行分组,方便绘制不同颜色的散点图
"""
x_red, x_blue, y_red, y_blue = [], [], [], []
for index in range(0, len(label)):
if label[index] == 1:
x_red.append(x_axis[index])
y_red.append(y_axis[index])
elif label[index] == -1:
x_blue.append(x_axis[index])
y_blue.append(y_axis[index])
return [x_red, x_blue], [y_red, y_blue]
def draw_table(x_axis, y_axis, label):
"""
显示最开始的分组结果
"""
axis_x, axis_y = get_scatter_data(x_axis, y_axis, label)
color = ['red', 'blue']
mark = ['1', '0']
for index in range(len(axis_x)):
plt.scatter(axis_x[index], axis_y[index], color=color[index], label=mark[index], alpha=.5)
plt.xlim((-4, 4))
plt.ylim((-3, 15))
plt.legend() # 显示图例
plt.show()
def table_line(x_axis, y_axis, label, omega, theta, i):
"""
绘制每次迭代时的超平面,并保存图片
:param x_axis: 样本的第一列
:param y_axis: 样本第二列
:param label: 样本标签【0,1】
:param omega: w
:param theta: θ
:param i: 迭代次数
:return:
"""
axis_x, axis_y = get_scatter_data(x_axis, y_axis, label)
color = ['red', 'blue']
mark = ['1', '0']
x1 = -theta / omega[0]
x2 = -theta / omega[1]
# 仅当可以绘制一条直线时,绘图
if x1 != x2:
for index in range(len(axis_x)):
plt.scatter(axis_x[index], axis_y[index], color=color[index], label=mark[index], alpha=.5)
plt.xlim((-4, 4))
plt.ylim((-3, 15))
plt.axline([x1, 0], [0, x2], label='超平面', color='black')
plt.legend() # 显示图例
# 将绘制的图保存到 result 目录下,用于制作 gif
plt.savefig('./result/images' + str(i) + '.jpg')
# 绘制完并保存后,关闭绘图,避免所有绘图绘制在一个图上
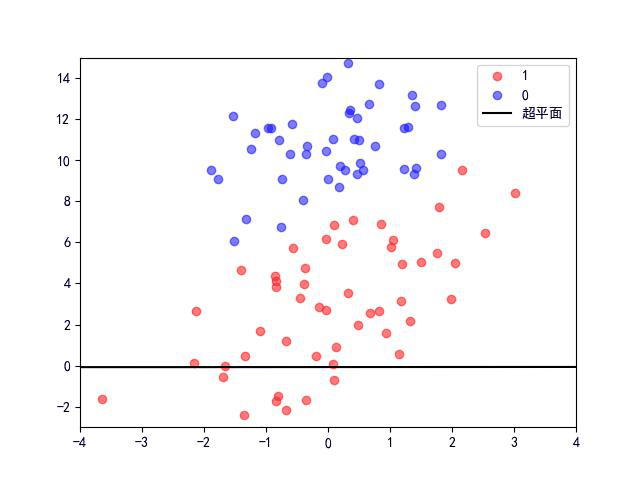
plt.close()为方便查看迭代过程中,随 $\omega,\theta$ 的变化而变化的超平面情况,将每次迭代后绘制超平面,然后将图片保存至 result 文件夹,再读取该文件夹所有文件,制作成一个 GIF,用于观看迭代变化情况。
实验结果
第 0 轮:
分类次数:1 θ: -0.50 w: [ 0.008806 -7.026532]
分类次数:2 θ: 0.00 w: [-0.689011 -4.6952615]
分类次数:3 θ: 0.50 w: [-0.485659 -1.161594]
分类次数:4 θ: 1.00 w: [-0.0604425 2.298573 ]
分类次数:5 θ: 0.50 w: [-0.734034 -4.289177]
分类次数:6 θ: 1.00 w: [-0.1456275 -2.705667 ]
分类次数:7 θ: 1.50 w: [-0.4289305 0.1688345]
分类次数:8 θ: 1.00 w: [-0.140668 -5.7206265]
分类次数:9 θ: 1.50 w: [-1.20291 -4.384391]
分类次数:10 θ: 2.00 w: [-1.0449175 -2.6224145]
分类次数:11 θ: 2.50 w: [-1.238079 -0.6277715]
分类次数:12 θ: 3.00 w: [-0.639777 1.848154]
分类次数:13 θ: 2.50 w: [-0.7773875 -2.9236695]
分类次数:14 θ: 3.00 w: [-1.0002265 -1.275018 ]
分类次数:15 θ: 3.50 w: [-0.4791155 1.7775595]
分类次数:16 θ: 3.00 w: [-0.169722 -3.3829335]
分类次数:17 θ: 3.50 w: [ 0.244545 -2.044911]
分类次数:18 θ: 4.00 w: [0.359273 0.916058]
分类次数:19 θ: 3.50 w: [ 0.8392155 -4.86161 ]
分类次数:20 θ: 4.00 w: [ 1.5928545 -2.347677 ]
分类次数:21 θ: 4.50 w: [1.64269 1.0702425]
分类次数:22 θ: 4.00 w: [ 1.814694 -4.2885 ]
分类次数:23 θ: 4.50 w: [ 2.707658 -0.4291775]
分类次数:24 θ: 4.00 w: [ 2.711255 -4.9670735]
分类次数:25 θ: 4.50 w: [ 3.7921 -0.2106735]
分类次数:26 θ: 4.00 w: [ 3.1437585 -6.014453 ]
分类次数:27 θ: 4.50 w: [ 2.4750225 -5.7802835]
分类次数:28 θ: 5.00 w: [ 2.4013605 -4.3428605]
分类次数:29 θ: 5.50 w: [ 3.0613325 -3.2572465]
分类次数:30 θ: 6.00 w: [ 4.0894405 -0.747256 ]
分类次数:31 θ: 6.50 w: [3.663624 1.4405895]
分类次数:32 θ: 6.00 w: [ 4.4186475 -1.5904065]
分类次数:33 θ: 6.50 w: [ 3.8689185 -0.7462695]
分类次数:34 θ: 6.00 w: [ 3.1688675 -7.06066 ]
分类次数:35 θ: 6.50 w: [ 4.0452885 -4.326577 ]
分类次数:36 θ: 7.00 w: [ 3.70539 -3.716312]
分类次数:37 θ: 7.50 w: [ 2.6209945 -3.644496 ]
第 1 轮:
分类次数:38 θ: 8.00 w: [ 1.9231775 -1.3132255]
分类次数:39 θ: 8.50 w: [2.1265295 2.220442 ]
分类次数:40 θ: 8.00 w: [ 1.7928325 -4.150284 ]
分类次数:41 θ: 8.50 w: [ 2.218049 -0.690117]
分类次数:42 θ: 8.00 w: [ 1.5444575 -7.277867 ]
分类次数:43 θ: 8.50 w: [ 2.132864 -5.694357]
分类次数:44 θ: 9.00 w: [ 1.849561 -2.8198555]
分类次数:45 θ: 9.50 w: [1.8374585 0.256056 ]
分类次数:46 θ: 9.00 w: [ 2.125721 -5.633405]
分类次数:47 θ: 9.50 w: [ 1.063479 -4.2971695]
分类次数:48 θ: 10.00 w: [ 1.2214715 -2.535193 ]
分类次数:49 θ: 10.50 w: [ 1.02831 -0.54055]
分类次数:50 θ: 10.00 w: [ 0.4158785 -6.33423 ]
分类次数:51 θ: 10.50 w: [ 1.0141805 -3.8583045]
分类次数:52 θ: 11.00 w: [ 0.7913415 -2.209653 ]
分类次数:53 θ: 11.50 w: [1.3124525 0.8429245]
分类次数:54 θ: 11.00 w: [ 1.621846 -4.3175685]
分类次数:55 θ: 11.50 w: [ 1.736574 -1.3565995]
分类次数:56 θ: 11.00 w: [ 2.4915975 -4.3875955]
分类次数:57 θ: 11.50 w: [ 3.9966725 -0.1867125]
分类次数:58 θ: 11.00 w: [ 3.2966215 -6.501103 ]
分类次数:59 θ: 11.50 w: [ 4.1730425 -3.76702 ]
第 2 轮:
分类次数:60 θ: 12.00 w: [ 3.4752255 -1.4357495]
分类次数:61 θ: 11.50 w: [ 3.19052 -6.210127]
分类次数:62 θ: 12.00 w: [ 3.6157365 -2.74996 ]
分类次数:63 θ: 12.50 w: [3.3324335 0.1245415]
分类次数:64 θ: 12.00 w: [ 3.620696 -5.7649195]
分类次数:65 θ: 12.50 w: [ 2.558454 -4.428684]
分类次数:66 θ: 13.00 w: [ 2.7164465 -2.6667075]
分类次数:67 θ: 13.50 w: [3.2375575 0.38587 ]
分类次数:68 θ: 13.00 w: [ 3.546951 -4.774623]
分类次数:69 θ: 13.50 w: [ 3.661679 -1.813654]
分类次数:70 θ: 13.00 w: [ 2.751131 -6.955649]
分类次数:71 θ: 13.50 w: [ 4.256206 -2.754766]
分类次数:72 θ: 14.00 w: [ 3.8328875 -0.8302285]
分类次数:73 θ: 13.50 w: [ 3.1328365 -7.144619 ]
分类次数:74 θ: 14.00 w: [ 4.0092575 -4.410536 ]
第 3 轮:
分类次数:75 θ: 14.50 w: [ 3.3114405 -2.0792655]
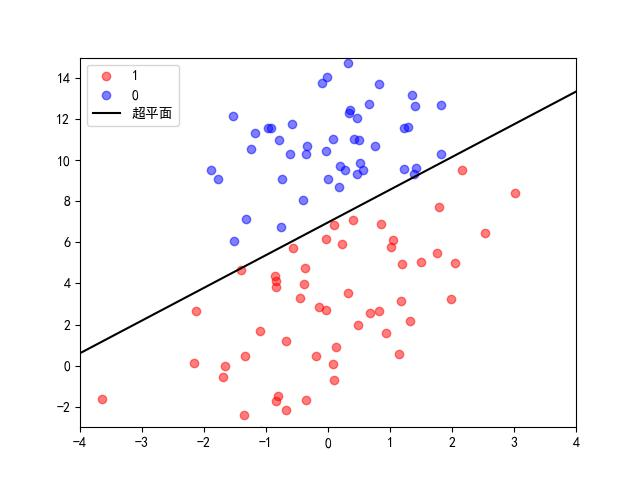
第 4 轮:超平面:
迭代过程:
实验心得体会
将数学公式转化成代码模型还是具有一定的难度呀,光看数学公式理解起来还是比较清晰的,但是如果靠自己将公式转化为代码模型就无从下手,只得先借鉴他人的成果,比如前文中的算法步骤,才好轻松进行转换。
其次是绘图的小问题,自己的想法是先绘制出散点图,再将直线加上去,然后获取第二张图,结果发现似乎没法实现。就只能每次都绘制散点,绘制直线,同时尽可能地减少代码的重复性。
后面调用 table_line() 函数绘制多个图时,发现,下一张图比上一张图多了一条直线,竟是每次在上一张图的基础上进行绘制,以致于图片全部作废,经了解,需要加上 ptl.close() “关闭” 图表,才好绘制新的图表。
实验参考
感知机学习算法
https://muxiner.github.io/ml-perceptron/