线性判别分析 —— 献血预测

实验原理

线性判别分析（LDA）

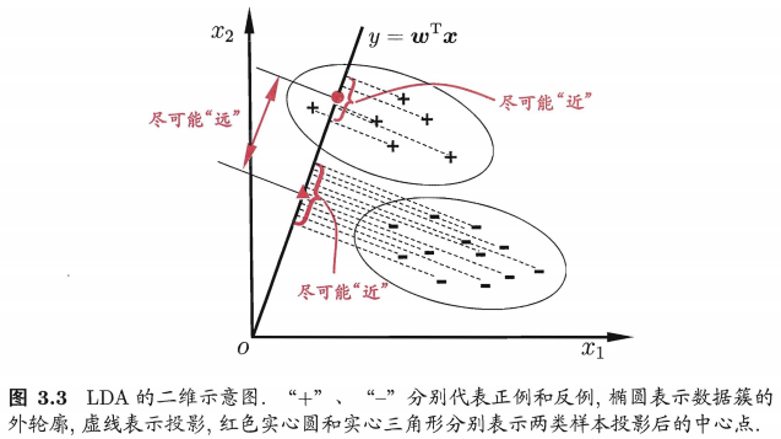
LDA 的思想非常朴素: 给定训练样例，设法将样例投影到一条直线上，使得同样例的投影点尽可能接近、异类样例的投影点尽可能远离;在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别.

数据集介绍

• 输血服务中心数据集：data/输血服务中心数据集/blood_data.txt
• 该实验是个分类问题。本数据集共有 748 个样本，5 个属性，详见 data/输血服务中心数据集/blood_names.txt

属性名	中文属性名	意义
R	近期	距离上次献血的月数
F	频率	捐献的总次数
M	度量	捐献的总血量
T	时间	距离首次献血的月数
Donate	一个二进制变量	表示他/她在是否在2007年3月献血（1：献血

实验要求

1. 划分测试集（600）和训练集（148），对数据集进行线性判别分析
2. 将模型结果的投影方向 w 进行输出
3. 输出测试集的准确率 acc
4. 最好能够将数据的分析结果进行可视化
5. 5 月 12 日晚上 12:00 之前将代码（.py 或者 .ipynb 文件）、实验报告（ doc 或 pdf 文件）一并打包上传至邮箱。

实验过程

加载数据

本部分主要工作：

1. 从 txt 文件中读取数据集
2. 将数据集分为 训练集 和 测试集
3. 将 训练集 和 测试集 分为 x， y 两个部分

主要代码：

def read_data(file_path, df_columns):
    # 读取 txt 到 datadfram。并加入列名
    data = pd.read_csv(file_path, header=None, sep=',')
    data.columns = df_columns
    return data

def load_data(file_path):
    """
    加载数据集，并划分训练集和测试集
    """
    data_columns = ['R', 'F', 'M', 'T', 'Donate']
    data_df = read_data(file_path, data_columns)
    # 训练集
    training_data = data_df.head(600)
    # 训练集 x, y
    training_x, training_y = training_data.iloc[:, :(training_data.shape[1] - 1)], training_data.iloc[:, -1]
    # 测试集
    testing_data = data_df.tail(148)
    # 测试集 x, y
    testing_x, testing_y = testing_data.iloc[:, :(testing_data.shape[1] - 1)], testing_data.iloc[:, -1]
    return training_x, training_y, testing_x, testing_y

编写 LDA 算法

本部分主要是计算下列的结果：

1. 计算类内散度矩阵 $S_w$
2. 计算类间散度矩阵 $S_b$
3. 计算矩阵 $S_w^{-1}S_b$
4. 计算 $S_w^{-1}S_b$ 的最大的 d 个特征值和对应的 d 个特征向量 （$w_1$, $w_2$, … $w_d$），得到投影矩阵 $W$

主要代码：
将 LDA 模型封装为一个类，该类需要传入三个参数：数据特征，数据标签以及降维后的维度。

• 数据特征：training_x
• 数据标签: training_y

变量定义：

• self.mu：样本的均值向量，$\mu$
• self.new_data：降维后的样本
• self.swt_sb：矩阵，$S_w^{-1}*S_b$，用于计算投影矩阵
• self.w：投影矩阵
• self.Sw：类内散度矩阵 $S_w$
• self.Sb：类间散度矩阵 $S_b$
• self.St：全局散度矩阵 $S_t$
• self.labels：数据标签，training_y 有的类型，本实验中共两种：0，1
• self.classify：第 $i$ 类的样本，$X_i$
• self.class_mu：第 $i$ 类样本的均值向量，$\mu_{i}$

class LDAModel(object):
    """
    线性判别分析
    """

    def __init__(self, data, target, d) -> None:
        """
        数据特征 数据标签 降维后的维度
        """
        self.data = data
        self.target = target
        self.d = d
        self.labels = set(target)
        # 列的平均值 μ
        # 所有样本的均值向量
        self.mu = self.data.mean(0)
        self.new_data = None
        self.swt_sb = None
        self.w = None
        self.Sw = None
        self.Sb = None
        self.St = None
        self.classify, self.class_mu = None, None

将样本根据标签进行分类：方便 $\mu_i$ 的计算

• $X_1$：献血的样本集，标签 1
• $X_2$：未献血的样本集，标签 0

  def data_divide_to_vectors(self):
      """
      功能：将传入的数据集按 target 分成不同的类别集合并求出对应集合的均值向量
      """
      self.classify, self.class_mu = {}, {}
      # 根据结果的值【0，1】，将训练样本分类：【0】一类，【1】一类
      for label in self.labels:
          # 分类
          self.classify[label] = self.data[self.target == label]
          # 均值向量(平均值)
          self.class_mu[label] = self.classify[label].mean(0)
  

  计算全局散度矩阵：全局散度矩阵实际上就是类内散度矩阵和类间散度矩阵之和
  $$S_t = S_b+S_w=\sum_{i = 1}^{m}(x_i-\mu)(x_i-\mu)^T$$

def get_st(self):
    """
    功能：计算全局散度矩阵
    """
    self.St = np.dot((self.data - self.mu).T, (self.data - self.mu))

计算类间散度矩阵：
类间散度矩阵其实就是协方差矩阵乘以样本数目，即散度矩阵与协方差矩阵只是相差一个系数。
$$S_b = \sum_{i=1}^Nm_i(\mu_i-\mu)(\mu_i-\mu)^T$$

def get_sb(self):
    """
    功能：计算类间散度矩阵
    """
    # 创建新的数组
    self.Sb = np.zeros((self.data.shape[1], self.data.shape[1]))
    for i in self.labels:
        # 获取类别i样例的集合
        class_i = self.classify[i]
        # 获取类别i的均值向量
        mu_i = self.class_mu[i]
        self.Sb += len(class_i) * np.dot((mu_i - self.mu).values.reshape(-1, 1),
                                         (mu_i - self.mu).values.reshape(1, -1))

计算类内散度矩阵：
重定义为了每个类别的散度矩阵之和。
$$S_w=S_t-S_b=\sum_{i=1}^NS_{w_i}=\sum_{i=1}^N\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T$$

def get_sw(self):
    """
    功能：定义类内散度矩阵
    """
    self.get_st()
    self.get_sb()
    # St = Sw + Sb
    self.Sw = self.St - self.Sb

计算 $S_w^{-1}*S_b$

def get_swt_sb(self):
    """
    计算 Sw^(-1)*Sb
    """
    self.data_divide_to_vectors()
    self.get_sw()
    self.swt_sb = np.linalg.inv(self.Sw).dot(self.Sb)

计算 $S_w^{-1}S_b$ 的特征值和特征向量，并取最大的 d 个特征值和对应的特征向量作为投影矩阵 $w$

def get_w(self):
    """
    功能：计算w
    """
    self.get_swt_sb()
    #  特征值 和 特征向量
    # eig_vectors[:i]与 eig_values相对应
    eig_values, eig_vectors = np.linalg.eig(self.swt_sb)
    # 寻找 d 个最大非零广义特征值
    top_d = (np.argsort(eig_values)[::-1])[:self.d]
    # 用d个最大非零广义特征值组成的向量组成w
    self.w = eig_vectors[:, top_d]

对测试集进行预测

主要代码：

def testing():
    """
    功能：对测试集进行分类并返回准确率
    """
    # 加载数据集
    train_x, train_y, test_x, test_y = load_data('./data/blood_data.txt')
    # print(train_x, test_x, train_y, test_y)
    # 创建模型
    lda = LDAModel(train_x, train_y, 1)
    # 获取投影矩阵w
    lda.get_result()
    # 对训练集进行降维
    train_x_handled = lda.new_data
    # 降维后的样本集
    # data_df = pd.concat([pd.DataFrame(train_x_handled), train_y], axis=1)
    # data_df.columns = ['Handled-Z1', 'Donate-Y1']
    # print(data_df)

    # 获取训练集各个类别对应的高斯分布的均值和方差
    gauss_dist = {}
    for i in lda.labels:
        category = train_x_handled[train_y == i]
        # 计算均值
        loc = category.mean()
        # 计算方差
        scale = category.std()
        gauss_dist[i] = {'loc': loc, 'scale': scale}
    # 测试集降维
    test_x_handled = np.dot(test_x, lda.w)
    pred_y = np.array([judge_classification(gauss_dist, x) for x in test_x_handled])

def judge_classification(gauss_dist, x):
    """
    功能：判断样本x属于哪个类别
    """
    # 将样本带入各个类别的高斯分布概率密度函数进行计算
    judge_result = [[k, norm.pdf(x, loc=v['loc'], scale=v['scale'])] for k, v in gauss_dist.items()]

    # 寻找计算结果最大的类别
    judge_result.sort(key=lambda s: s[1], reverse=True)
    # print(judge_result)
    return judge_result[0][0]

def accuracy_score(y_true, y_pred):
    """
    Compare y_true to y_pred and return the accuracy
    比较 实际值 与 预测值，并返回准确度
    """
    accuracy = np.sum(y_true == y_pred, axis=0) / len(y_true)
    return accuracy

绘制图标

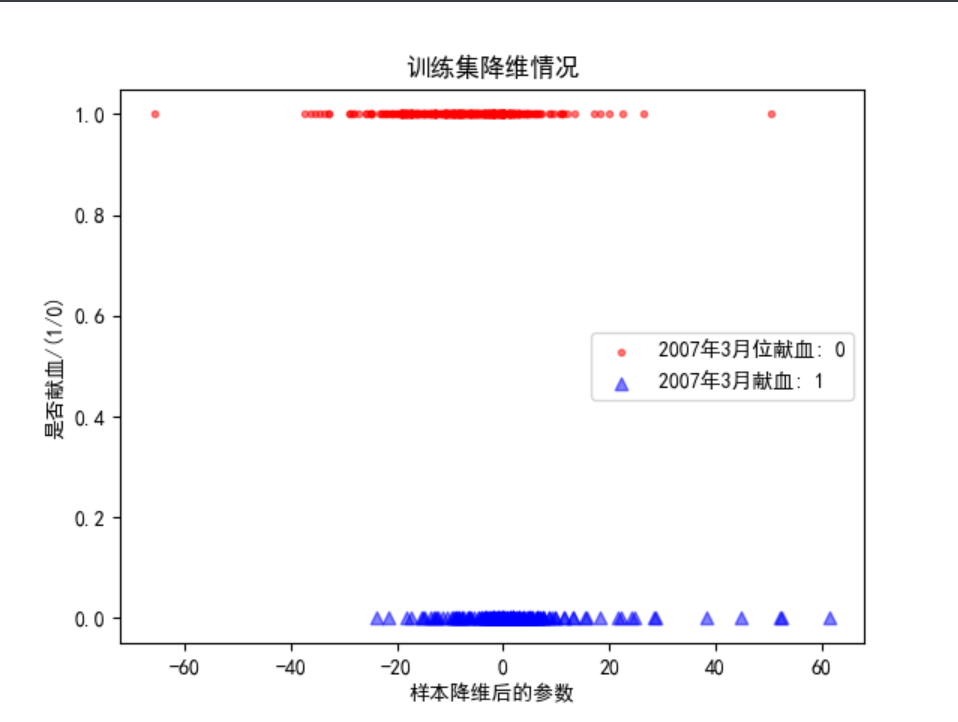
绘制训练集降维后的图表，以降维结果作为横坐标，0|1作为纵坐标。

本图重在表示降维后，两类样本的位置情况。

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.scatter(train_x_handled[train_y == 0], np.ones((1, train_x_handled[train_y == 0].shape[0])),
            marker='.', color='red', label='2007年3月位献血: 0', alpha=0.5)
plt.scatter(train_x_handled[train_y == 1], np.zeros((1, train_x_handled[train_y == 1].shape[0])),
            marker='^', color='blue', label='2007年3月献血: 1', alpha=0.5)
plt.legend()
plt.title("训练集降维情况")
plt.ylabel("是否献血/(1/0)")
plt.xlabel("样本降维后的参数")
plt.show()

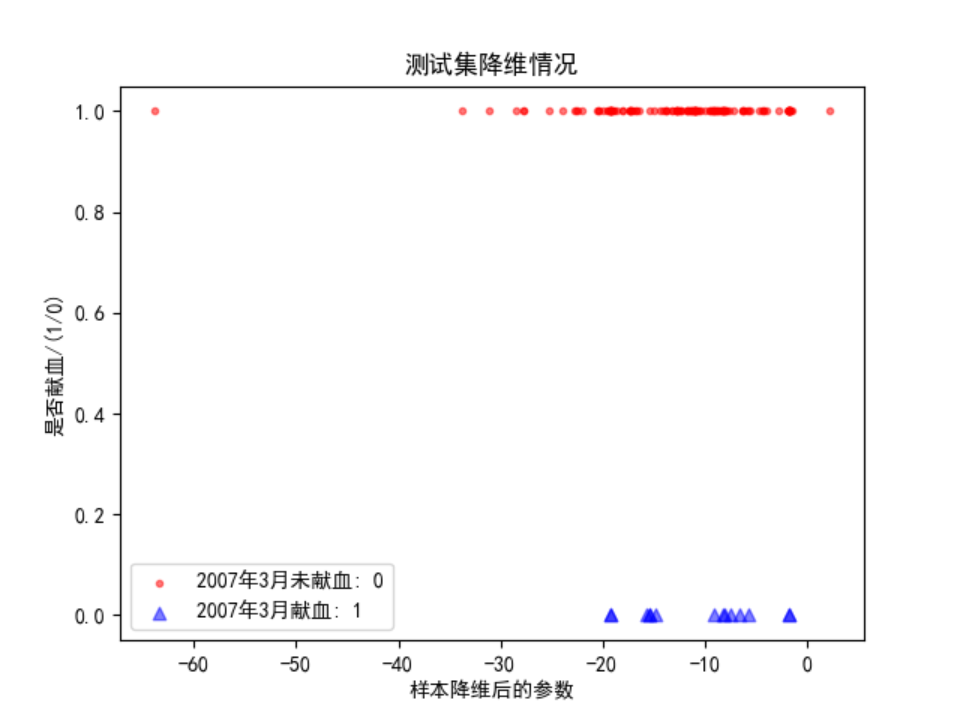
绘制测试集降维后的图表，以降维结果作为横坐标，0|1作为纵坐标。

本图重在表示降维后，两类样本的位置情况。

plt.scatter(test_x_handled[test_y == 0], np.ones((1, test_x_handled[test_y == 0].shape[0])),
               marker='.', color='red', label='2007年3月未献血: 0', alpha=0.5)
   plt.scatter(test_x_handled[test_y == 1], np.zeros((1, test_x_handled[test_y == 1].shape[0])),
               marker='^', color='blue', label='2007年3月献血: 1', alpha=0.5)
   plt.legend()
   plt.title("测试集降维情况")
   plt.ylabel("是否献血/(1/0)")
   plt.xlabel("样本降维后的参数")
   plt.show()

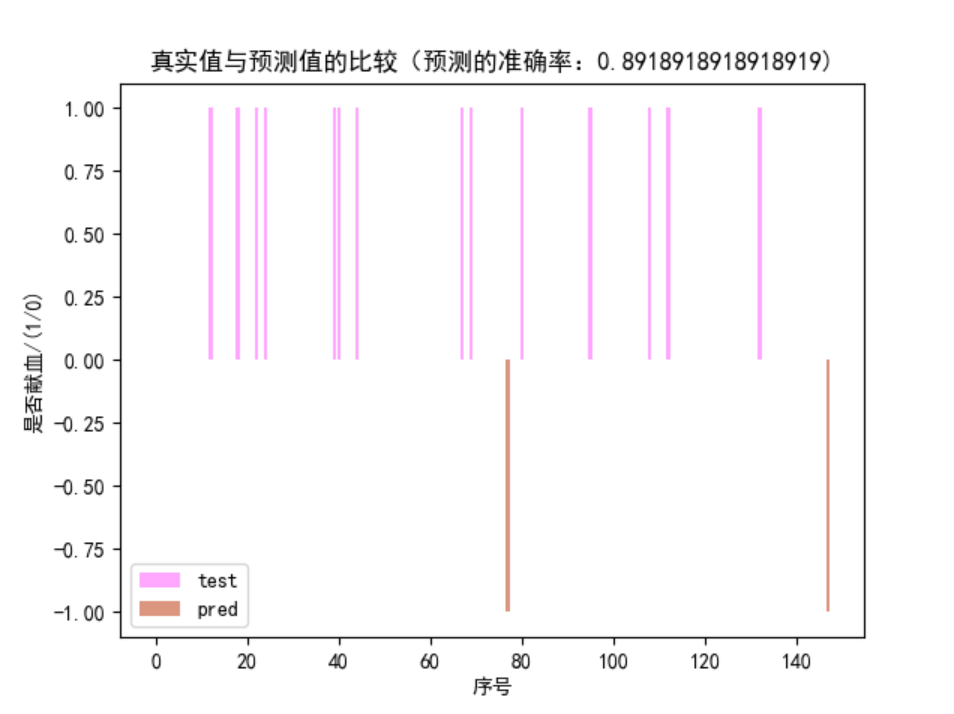
绘制测试集的预测值与真实值的比较图表。

横坐标是序号，0~148

纵坐标是 0 | -1 | +1，0表示未献血，+1 表示真实值的献血，-1表示预测值的献血

该图结果是，具有不同颜色条形的图表，当某一序号位置某颜色的条形不存在同序号位置的另一色的条形，表示该序号位置的预测值与真实值不一致。

由图可得准确率：$1-frac{\text{位置不一致的条形个数}}{148}$

y1 = test_y
y2 = pred_y
x = range(0, 148)
plt.scatter(x, y1, color='#ff4eff', label='test', alpha=0.5)
plt.scatter(x, -y2, marker='^', color='#ba2c01', label='pred', alpha=0.5)
plt.legend()
plt.title("真实值与预测值的比较（预测的准确率：" + str(accuracy_score(test_y, pred_y)) + ")")
plt.ylabel("是否献血/(1/0)")
plt.xlabel("序号")
plt.show()

实验结果

将投影矩阵与预测准确度写入了 ./output.txt 中。文件内容如下：

训练结果(w)： [[-0.59843282  0.73633892  0.00455796 -0.31569349]]
预测准确度： 0.8918918918918919

实验总结

本次实验实践了线性判别分析算法。

经过查阅资料、上手实践后，对线性判别分析（LDA）算法有了一定的了解：

• LDA 有二分类、多分类两种情况

  二分类也可是多分类的特殊情况。
  二分类和多分类在公式表达上略有不同。
  二者的算法思路、步骤一致。

• LDA 步骤：
  1. 计算类内散度矩阵 $S_w$
  2. 计算类间散度矩阵 $S_b$
  3. 计算矩阵 $S_w^{-1}S_b$
  4. 计算 $S_w^{-1}S_b$ 的最大的 d 个特征值和对应的 d 个特征向量 （$w_1$, $w_2$, … $w_d$），得到投影矩阵 $W$
  5. 计算 降维后的样本 $Z_i = X_i * w$

实验的实现还是基于明白数学公式，这还是实验的重难点哦。

还有一点就是，选择一个合适的图表用来表示可视化的结果也是有点难度的。

实验参考

• Python机器学习笔记：线性判别分析（LDA）算法
• 机器学习(三)：一文读懂线性判别分析（LDA）
• 机器学习实战笔记5——线性判别分析