决策树 —— 隐形眼镜数据集预测
本文最后更新于:2022年6月28日星期二晚上10点39分
实验原理
决策树思想
决策树学习的本质:从训练数据集中归纳出一组分类规则。
可能这种决策规则一个也没有
也可能有多个决策规则
此时需要选择一个与数据集矛盾较小的决策树规则,同时有需要很好的泛化效果。
学习算法原理
- 构造根节点,将所有的训练数据集放入根节点
- 选择一个最优特征,将训练集分割成子集,使得训练及在当前条件下有最好的分类
- 如果这些子集已经可能很好的分类,那么构建叶子节点;如果还不能很好的分类,继续对其分割,构造相应的节点
- 重复(递归)进行上述步骤,直至所有训练数据集被基本正确分类,或者没有合适的特征为止
经过以上过程,决策树可能对训练集有了很好的分类能力,但是对未知数据不一定同样有很好的分类效果。
所以,为了避免过拟合现象,还需要对生成的树进行剪枝,将树变得更简单,以实现更好的泛化能力。
从上面可以看出,一个决策树学习算法需要包括特征选取、决策树生成和决策树剪枝过程。
常用的学习算法有:
ID3[Quinlan, 1986]:最优特征选择标准是信息增益
ID4.5[Quinlan, 1993]:最优特征选择标准是信息增益率
CART[Breiman, 1984]:最有特征选择标准是节点方差的大小
决策树学习基本算法
信息增益率
增益率(gain ratio)
$$
Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}
$$
其中
$$
IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|}
$$
称为属性 a 的“固有值”(intrinsic value)[Quinlan, 1993]。
属性 a 的可能取值数目越多(即 V 越大),则 IV(a) 的值通常会越大。
近看上述公式,并不是很明白增益率如何计算。查阅资料后知,分为几步:
- 计算整体的信息熵
$$
H(X) = -\sum_{i = 1}^{m}p_ilog_2(p_i)
$$
- $m$: 训练数据集结果的标签数
- $p_i$: 第 $i$ 类标签的比例
- 计算某特征的条件熵
$$
H(X|Y)=\sum_{y\in Y}p(y)H(X|Y=y)
$$
$H(X|Y=y)$: 该特征中某标签的条件熵
$$
H(X|Y = y_i) =-\sum_{i=1}^{n}p_ilog_2(p_i)
$$$n$: 在条件为该特征中某标签下,结果的标签数
$p_i$: 在条件为该特征中某标签下,第 $i$ 类结果标签的比例
计算某特征的信息增益
$$
g(X,Y)=H(X)-H(X|Y)
$$计算某特征的内部信息(Intrinsic Information of an Attribute)
其实就是特征的信息熵
$$
Intl(X,Y)=-\sum_{i=1}^{m}\frac{|Y_i|}{|X|}log_2(\frac{|Y_i|}{|X|})
$$
- $Y$: 表示某个特征的随机变量
- $Y_i$: 该特征的第 $i$ 类的个数
- $X$: 表示样本的总个数
- $\frac{|Y_i|}{|X|}$: 表示该特征的第 $i$ 类占样本的比例
- 计算某特征的信息增益率
$$
g(X|Y)=\frac{g(X,Y)}{Intl(X,yY)}
$$
结合实例理解请详见:信息增益率
决策树算法框架
决策树主函数
各类决策树的主函数都大同小异,本质上是一个递归函数。
该函数的主要功能是按照某种规则生长出决策树的各个分支节点,并根据终止条件结束算法。
一般来讲,主函数需要完成如下几个功能:
- 输入需要分类的数据集和类别标签
- 根据某种分类规则得到最优的划分特征,并创建特征的划分节点 —— 计算最优特征子函数
- 按照该特征的每个取值划分数据集为若干部分 —— 划分数据集子函数
- 根据划分子函数的计算结果构建出新的节点,作为树生长出的新分支
- 检验是否符合递归的终止条件
- 将划分的新节点包含的数据集和类别标签作为输入,递归执行上述步骤。
计算最优特征子函数
计算最优特征子函数是除主函数外最重要的函数。
每种决策树之所以不同,一般都是因为最优特征选择的标准不同,不同的标准导致不同类型的决策树。如:
ID3[Quinlan, 1986]:最优特征选择标准是信息增益ID4.5[Quinlan, 1993]:最优特征选择标准是信息增益率CART[Breiman, 1984]:最有特征选择标准是节点方差的大小
划分数据集子函数
划分数据集函数的主要功能是分隔数据集,有的需要删除某个特征轴所在的数据列,返回剩余的数据集;有的干脆将数据集一分为二。
分类器
所有的机器学习算法都要勇于分类或回归预测。
决策树的分类器就是通过遍历整个决策树,使测试集数据找到决策树中叶子节点对应的类别标签。这个标签就是返回的结果。
数据集介绍
数据集:
隐形眼镜数据集/lenses_data.txt
共有 24 个样本:- 4 个输入变量(数据集中第一列为样本编号)
- 1 个输出变量(数据集中最后一列)
数据集信息:
- 3 类结果标签:
1:患者应佩戴硬隐形眼镜2:患者应佩戴软性隐形眼镜3:患者不应佩戴隐形眼镜
- 4 类特征及其标签
- 年龄:
1:青年2:中年3:老年
- 症状:
1:近视2:远视
- 散光:
1:否2:是
- 眼泪数量:
1:减少2:正常
- 年龄:
- 详见
隐形眼镜数据集/lenses_names.txt
- 3 类结果标签:
实验环境
Python版本:Python 3.6- 编辑器:
PyCharm - 扩展包:
numpy、pandas、matplotlib等基础扩展包不可使用
sklearn、kreas等机器学习包
实验要求
- 采用
C4.5算法建立决策树模型 - 将每个特征的信息增益率打印输出
- 输出最后建立的决策树模型结构图(可以用
字典结构表示,也可以用matplotlib等图形库绘制出树形图)- 字典表示:

- 树形图表示:
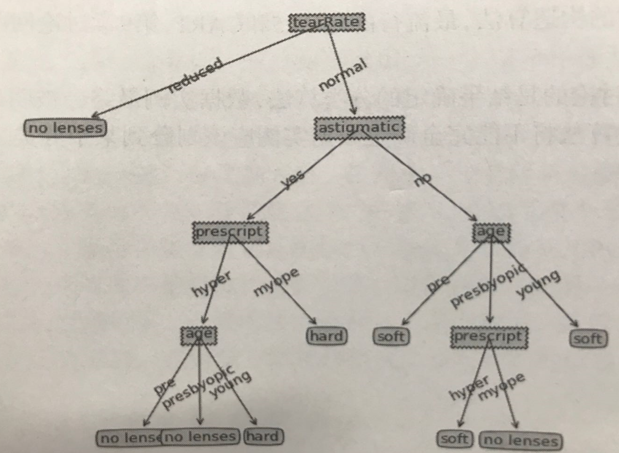
- 字典表示:
实验代码详解
读取数据文件
简单的使用 numpy.loadtxt 读取 txt 的后五行数据。
一开始读取完数据后还分一下训练集、测试集的,后面发现,这数据是有规律的,就像是四类特征的标签进行了笛卡尔积运算一行,结果的标签也具有一点点的规律。
又仔细看了看实验要求,没说需要预测,只是说需要 信息增益率 + 决策树结构。
所以就,不分训练集和测试集。
最优特征子函数 —— 信息增益率计算
该部分主要是计算各特征的信息增益率,并进行比较,返回信息增益率最大的特征的索引。
该计算也分为几步:
- 计算标签信息熵:对应函数
get_info_entropy(x) - 计算条件信息熵:对应函数
get_conditional_info_entropy(feature, x) - 计算信息增益率:对应函数
get_info_gain_ratio(feature, x) - 获取最佳信息增益率的索引:对应函数
get_best_feature(data, label, is_print)
计算均按照上述公式
数据集划分子函数
该部分就是在递归时,获取作为递归参数 —— 数据集。
该数据集的特征有:
- 缺少上一次递归时最佳特征所在的那一列
- 缺少的这一列的值均相同
就是:
该函数会根据最佳特征的标签的情况将数据集划分为 $m$ 类。
$m$ 是最佳特征标签的个数。
每类子数据集都是最佳特征标签相同的其他特征数据的集合。
def split_dataset(data, index, value):
"""
对数据集进行分片
:param data: 需要分片的数据集
:param index: 新数据集不需要的某列的索引
:param value: 用于确定新数据集需要某行在 某列[index]对应的值
:return: 新的数据集
"""
has_split_dataset = []
for col_data in data:
# 选择特定行的数据进行切片
if col_data[index] == value:
# 取 第 index 个前的所有元素
has_split_col = col_data[:index].tolist()
# 再加上第 index 个后面的所有元素
has_split_col.extend(col_data[index + 1:].tolist())
# 再将其加入 新的 数据集
has_split_dataset.append(has_split_col)
return np.array(has_split_dataset)决策树主函数
获取数据集中的标签数据:labels = [item[-1] for item in data]
递归终止条件
子节点的样本属于同一类标签
返回该类标签
if 1 == len(set(labels)): return labels[0]子节点样本的特征标签相同,或是没有了样本
返回出现次数最多的标签
# 特征集为空 或是 特征集上的取值相同,停止分类 # 返回出现次数最多的 标签 # len(data[0]) == 1 就是数据集里只剩下标签,没有特征了 # len(set(data[:, 0])) == 1 特征集上的取值相同 # not feature_label 特征集空了 if len(data[0]) == 1 or len(set(data[:, 0])) == 1: return most_label(labels) def most_label(data): """ 返回,出现次数最大多的标签 """ label = list(set(data)) most = '' most_count = 0 for item_label in label: count = 0 for item_data in data: if item_label == item_data: count += 1 most = item_label if count > most_count else most most_count = count return most ```Glasses 3. 特征集为空 返回出现次数最多的标签 ```python if not feature_label: return most_label(labels)
创建节点
- 通过最优特征子函数获取最优特征的索引
- 根据索引从特征集中获取最有特征
- 将最优特征添加到决策树中
- 删除特征集中的最优特征
该删除并非真的删除,而是进入递归时,进入递归的特征集不包含最优特征
# 从特征标签中选择最优划分标签
# 选择最优标签
best_index = get_best_feature(data[:, 0:-1], np.array(labels), False)
# 获取最优的标签
best_feature_label = feature_label[best_index]
# 根据最优特征的标签生成树
decision_tree = {best_feature_label: {}}
# 删除已使用的标签
# del (feature_label[best_index])创建分支
- 获取数据集中最优特征的所有数据
- 根据数据获取特征标签
- 根据特征标签创建分支
- 进入递归:
- 划分数据集,作为递归中的数据集参数
- 划分特征集,作为递归中的特征集参数
# 得到训练集中所有最优特征的标签
feat_value = [item[best_index] for item in data]
# 去掉重复值
for value in set(feat_value):
decision_tree[best_feature_label][value] = create_decision_tree(
split_dataset(data, best_index, value),
split_feature(feature_label, best_index))两个划分函数:
def split_dataset(data, index, value):
"""
对数据集进行分片
:param data: 需要分片的数据集
:param index: 新数据集不需要的某列的索引
:param value: 用于确定新数据集需要某行在 某列[index]对应的值
:return: 新的数据集
"""
has_split_dataset = []
for col_data in data:
# 选择特定行的数据进行切片
if col_data[index] == value:
# 取 第 index 个前的所有元素
has_split_col = col_data[:index].tolist()
# 再加上第 index 个后面的所有元素
has_split_col.extend(col_data[index + 1:].tolist())
# 再将其加入 新的 数据集
has_split_dataset.append(has_split_col)
return np.array(has_split_dataset)
def split_feature(label, index):
error_deal = []
for i in range(0, len(label)):
if i != index:
error_deal.append(label[i])
return error_deal返回决策树
当分支创建完毕后,就返回决策树。
实验结果
实验结果输出各特征的信息增益率和决策树模型(元组结构)。
信息增益率:
第 1 个特征的信息增益率为 0.02485642633702430
第 2 个特征的信息增益率为 0.03951083542356582
第 3 个特征的信息增益率为 0.37700523001147723
第 4 个特征的信息增益率为 0.54879494069539858决策树模型(手动进行了格式化处理):
{
'眼泪数量':
{
1: 3,
2:
{
'散光':
{
1:
{
'年龄':
{
1: 2,
2: 2,
3:
{
'症状':
{
1: 3,
2: 2
}
}
}
},
2:
{
'症状':
{
1: 1,
2:
{
'年龄':
{
1: 1,
2: 3,
3: 3
}
}
}
}
}
}
}
}文件中显示的为:
{‘眼泪数量’: {1: 3, 2: {‘散光’: {1: {‘年龄’: {1: 2, 2: 2, 3: {‘症状’: {1: 3, 2: 2}}}}, 2: {‘症状’: {1: 1, 2: {‘年龄’: {1: 1, 2: 3, 3: 3}}}}}}}}
结果均输出在
output.txt文件中。
实验心得体会
实验就,很有意思。
遇到的问题及解决办法
主要是递归终止条件上的问题,未能很好的明确递归终止的条件,经过一番查询及自己思考后,明确了四个条件:
- 子节点的样本属于同一类标签:返回该类标签
- 子节点样本的特征标签相同:返回出现次数最多的标签
- 子节点没有样本:返回出现次数最多的标签
- 特征集为空:返回出现次数最多的标签
总的就算两种情况下的终止条件:
- 返回出现次数最多的标签:子节点样本的特征标签相同、子节点没有样本、特征集为空
- 返回该类标签:子节点的样本属于同一类标签
还有一个问题就是,也是浪费时间比较多的问题:特征集在递归中会提前为空,以至于在子节点中的样本还没有完全分类时,就提前结束了递归,返回了决策树。
此时的实验结果是:
{‘眼泪数量’:{1: 3,2:{‘散光’:{1:{‘年龄’:{1: 2,2: 2,3:{‘症状’:{1: 3,2: 2}}}},2: 1}}}}
仔细审查后发现是特征集在里层递归改变后,外层的递归中也发生了改变。虽然发现了上述问题的原因,但是并没有明白导致该问题是因为什么。
经过一番思索获得了解决问题的方法,然后得到下面的结果:
{‘眼泪数量’: {1: 3, 2: {‘散光’: {1: {‘年龄’: {1: 2, 2: 2, 3: {‘年龄’: {1: 3, 2: 2}}}}, 2: {‘症状’: {1: 1, 2: {‘年龄’: {1: 1, 2: 3, 3: 3}}}}}}}}
{‘眼泪数量’: {1: 3, 2: {‘散光’: {1: {‘年龄’: {1: 2, 2: 2, 3: {‘症状’: {1: 3, 2: 2}}}}, 2: {‘年龄’: {1: 1, 2: {‘症状’: {1: 1, 2: 3, 3: 3}}}}}}}}
但是并不能解决问题。
后面根据自己仔细地、一步步试错,发现是特征集的数据类型,在经过删除操作后,会改变其他所有后续执行中的特征集。
这也就是为什么“特征集在递归中会提前为空,以至于在子节点中的样本还没有完全分类时,就提前结束了递归,返回了决策树”。
此时便想起特征集的内存地址都是一样的,无论什么操作都是对同一内存地址上的数据进行操作,也就导致这里动、那里变,就导致“特征集提前为空”。
然后查看特征集的数据类型 —— list,列表,一查其存储方式,果然如此
列表如何存储?
列表本质是动态的数组,列表存储的是每个元素在内存中的地址(即引用),当列表中空白占位低于1/3时,会在内存中开辟一块更大的空间,并将旧列表中存储的地址复制到新列表中,旧列表则被销毁,这样就实现了扩容。因为列表存储的是元素的引用这个特性,而引用所占的内存空间是相同的,这样便可以同时存放不同类型的数据了。