多元线性回归 —— 波士顿房价预测

本文最后更新于：2022年6月28日星期二晚上10点39分

实验原理

多元线性回归——最小二乘法

数据集介绍

波士顿房价数据集

数据集的获得:

  • 下载

  • 通过包导入

    下载获得数据集有点小问题，因而我是用的 包导入。

    from sklearn import datasets
boston = datasets.load_boston()
# 将房价信息转成dataFrame格式
df_boston_house_data = pd.DataFrame(boston.data, columns=boston.feature_names)
df_boston_house_data['PRICE'] = boston.target
# 查看数据是否存在空值，从结果来看数据不存在空值。
# print(df_boston_house_data.isnull().sum())
# 查看数据大小
# print(df_boston_house_data.shape)
# 显示数据前5行
# print(df_boston_house_data.head())
# 将数据集写入csv文件
df_boston_house_data.to_csv("boston_housing_data.csv", index=False, sep=',')

  • 该数据集是一个回归问题。每个类的观察值数量是均等的，共有 506 个观察，13 个输入变量（数据集中前13列）和1个输出变量（最后一列）。

  • 每条数据包含房屋以及房屋周围的详细信息。其中包含城镇犯罪率，一氧化氮浓度，住宅平均房间数，到中心区域的加权距离以及自住房平均房价等等。

属性名 解释 类型
CRIM 该镇的人均犯罪率 连续值
ZN 占地面积超过25,000平方呎的住宅用地比例 连续值
INDUS 非零售商业用地比例 连续值
CHAS 是否邻近 Charles River（查尔斯河） 离散值，1=邻近；0=不邻近
NOX 一氧化氮浓度 连续值
RM 每栋房屋的平均客房数 连续值
AGE 1940年之前建成的自用单位比例 连续值
DIS 到波士顿5个就业中心的加权距离 连续值
RAD 到径向公路的可达性指数 连续值
TAX 全值财产税率 连续值
PTRATIO 学生与教师的比例 连续值
B $1000(BK - 0.63)^2$，其中BK为黑人占比 连续值
LSTAT 低收入人群占比 连续值
MEDV 同类房屋价格的中位数 连续值

实验详解


简单的说就是，本次实验需要求得是：
$$
f(x)=w_1x_1 + w_2x_2+…+w_dx_d+b
$$
中的 $w_1,w_2,…,w_d,b(d=13)$，然后通过这 14 个参数与测试集的前 13 个变量进行计算，求得预测的房价。

参数使用下列算式计算：
$$
w^* = (X^TX)^{-1}X^Ty
$$
其中：

  • $w^*$：是所求的参数组成的一列矩阵
  • $X$: 训练集前 13 列变量组成的矩阵
  • $y$: 训练集第 14 列变量组成的矩阵
  • $X^T$：$X$ 的转置矩阵

实验环境

  • Python 3.9
  • 编辑器：Pycharm
  • 可使用 numpy、pandas、matplotlib 等基础扩展包，建议使用 anaconda 安装
  • 不可使用 sklearn、pytorch 等机器学习包

实验要求

  1. 将数据集拆分成训练集（前 450 个样本）和测试集（后 56 个样本）
  2. 利用多元线性回归模型（最小二乘法或者梯度下降法均可）对训练数据进行拟合
  3. 对拟合得到的模型在测试集上进行测试，使用均方误差作为实验的准确结果并输出。

实验过程

  1. 数据集获得
    使用 sklearn 包导入数据集，但是仅仅是导入，写入 csv 文件，后续使用的数据集均是从 csv 文件读取的。
    from sklearn import datasets
boston = datasets.load_boston()
# 将房价信息转成dataFrame格式
df_boston_house_data = pd.DataFrame(boston.data, columns=boston.feature_names)
df_boston_house_data['PRICE'] = boston.target
# 查看数据是否存在空值，从结果来看数据不存在空值。
# print(df_boston_house_data.isnull().sum())
# 查看数据大小
# print(df_boston_house_data.shape)
# 显示数据前5行
# print(df_boston_house_data.head())
# 将数据集写入csv文件
df_boston_house_data.to_csv("boston_housing_data.csv", index=False, sep=',')
  2. 读取数据集
    def read_data(file_path):
 """
 从文件路径中读取数据集
 :param file_path: 文件路径
 :return: 返回一个 dataFrame
 """
 return pd.read_csv(file_path, sep=',')
  3. 数据集拆分为训练集和测试集
    def get_training_data(df, num):
 """
 从 df 中获得训练集
 :param num:
 :param df:
 :return:
 """
 # 取测试集的前450项
 df_training = df.head(num)
 return df_training

 def get_test_data(df, num):
 """
 从 df 中获取测试集
 :param df:
 :param num:
 :return:
 """
 # 取数据集的后50项
 df_test = df.tail(num)
 return df_test
  4. 计算学习的模型
    通过公式进行计算。
    $$w^* = (X^TX)^{-1}X^Ty$$
    def model_calculation(df_x, df_y):
 """
 计算模型
 :param df_x:
 :param df_y:
 :return:
 """
 # 定义大小为 450 的全1数组，用于在 X 矩阵前插入一列全 1 的数
 one_matrix = np.full(len(df_x), 1, dtype=int)
 # X 第一列插入 一列 1，获得 X 矩阵
 x_matrix = np.insert(dataframe_to_matrix(df_x), 0, values=one_matrix, axis=1)
 # y 矩阵
 y_matrix = dataframe_to_matrix(df_y)
 # X，y 通过计算获得 β 参数
 beta = np.dot(np.linalg.inv(np.dot(x_matrix.T, x_matrix)), np.dot(x_matrix.T, y_matrix))
 
 return beta
  5. 通过模型获得房价预测值
    def get_estimate(beta, df_test):
 """

 :param beta: β的矩阵
 :param df_test: 测试集
 :return: 返回预测价格的矩阵（数组）
 """
 # 先定义预测值的数组，大小等于测试样例大小，用0填充
 estimate = np.full(len(df_test), 0, dtype=int)
 # 定义大小为56的全1数组，用于在 X 矩阵前插入一列全 1 的数
 one_matrix = np.full(len(df_test), 1, dtype=int)
 # 将测试集中的前13项作为 矩阵 X 的数
 test_matrix = dataframe_to_matrix(get_not_last_column(df_test))
 # X 第一列插入 一列 1
 test_matrix = np.insert(test_matrix, 0, values=one_matrix, axis=1)
 # print(np.size(test_matrix, 0))
 # X 中每一行同 β进行计算，获得预测的价格
 for i in range(np.size(test_matrix, 0)):
     estimate[i] = np.dot(beta, test_matrix[i])

 # print(estimate)
 return estimate
  6. 绘制房价实际值和预测值的比较图
    # 绘制预测值与真实值图
 # 规定字体，避免乱码
 plt.rcParams['font.sans-serif'] = [u'SimHei']
 plt.rcParams['axes.unicode_minus'] = False
 plt.plot(true_value_price, color="r", label="实际价格")  # 颜色表示
 plt.plot(estimate_value_price, color=(0, 0, 0), label="预测价格")
 plt.xlabel("测试序号")  # x轴命名表示
 plt.ylabel("价格")  # y轴命名表示
 plt.title("实际值与预测值折线图")
 plt.legend()  # 增加图例
 plt.show()  # 显示图片

实验结果

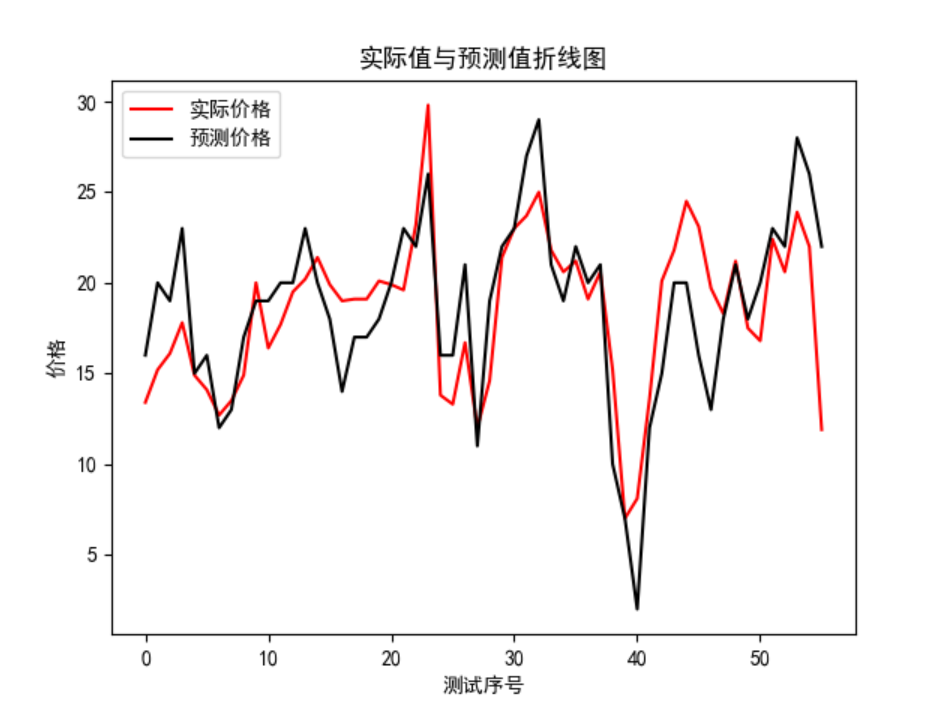
分析：

上述结果仅是一次学习的结果，可见 50 组实际值与预测值之间出入较大，大部分的实际值与预测值之间存在较大的差别。

不过好在获得了想要的结果。

实验总结

本次实验是机器学习中的第一次尝试，简单又不是难度。

简单在于，了解实验如何运作后，实现起来还是特别简单的，确实不需要什么数学，当然，前提是，能够看懂如何从数学转换到 python 的代码。

难度在于，“万事开头难”，以及需要看懂最小二乘法是怎么运作的。

最后，机器学习还是非常的有趣，值得一直取尝试。

参考资料

实验完整代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets


# 数据集下载地址：https://www.kaggle.com/datasets/altavish/boston-housing-dataset?resource=download


def get_boston_house_data():
    """
    从包中加载波士顿房价数据集
    （本不知道有这种包，但是发现下载的数据集在操作上都存在一些问题，因而找到这种方法）
    :return:
    """
    # 加载波士顿房价数据集信息
    boston = datasets.load_boston()
    # 将房价信息转成dataFrame格式
    df_boston_house_data = pd.DataFrame(boston.data, columns=boston.feature_names)
    df_boston_house_data['PRICE'] = boston.target
    # 查看数据是否存在空值，从结果来看数据不存在空值。
    # print(df_boston_house_data.isnull().sum())
    # 查看数据大小
    # print(df_boston_house_data.shape)
    # 显示数据前5行
    # print(df_boston_house_data.head())
    # 将数据集写入csv文件
    df_boston_house_data.to_csv("boston_housing_data.csv", index=False, sep=',')
    # return df_boston_house_data


def get_data_describe(df):
    """

    :param df:
    :return:
    """
    # 查看数据的描述信息，在描述信息里可以看到每个特征的均值，最大值，最小值等信息
    df.describe()


def read_data(file_path):
    """
    从文件路径中读取数据集
    :param file_path: 文件路径
    :return: 返回一个 dataFrame
    """
    return pd.read_csv(file_path, sep=',')


def get_training_data(df, num):
    """
    从 df 中获得训练集
    :param num:
    :param df:
    :return:
    """
    # 取测试集的前450项
    df_training = df.head(num)
    # print(df_training)
    return df_training


def get_test_data(df, num):
    """
    从 df 中获取测试集
    :param df:
    :param num:
    :return:
    """
    # 取数据集的后50项
    df_test = df.tail(num)
    # print(df_test)
    return df_test


def get_last_column(df):
    """
    获取df最后一列的数据
    :param df:
    :return:
    """
    # print(df.iloc[:, -1])
    return df.iloc[:, -1]


def get_not_last_column(df):
    """
    获取df的除最后一列的所有数据
    :param df:
    :return:
    """
    # print(len(df))
    # print(df.iloc[:, :(df.shape[1] - 1)])
    return df.iloc[:, :(df.shape[1] - 1)]


def dataframe_to_matrix(df):
    """
    将df转换为多维矩阵
    其实就是转为 numpy 数组
    :param df: 需要转换的 df
    :return:
    """
    return df.to_numpy()


def model_calculation(df_x, df_y):
    """
    计算模型
    :param df_x: 训练集的前13列
    :param df_y: 训练集的第14列
    :return:
    """
    # 定义大小为 450 的全1数组，用于在 X 矩阵前插入一列全 1 的数
    one_matrix = np.full(len(df_x), 1, dtype=int)
    # X 第一列插入 一列 1，获得 X 矩阵
    x_matrix = np.insert(dataframe_to_matrix(df_x), 0, values=one_matrix, axis=1)
    # y 矩阵
    y_matrix = dataframe_to_matrix(df_y)
    # X，y 通过计算获得 β 参数
    beta = np.dot(np.linalg.inv(np.dot(x_matrix.T, x_matrix)), np.dot(x_matrix.T, y_matrix))
    # print(beta)
    return beta


def get_estimate(beta, df_test):
    """

    :param beta: β的矩阵
    :param df_test: 测试集
    :return: 返回预测价格的矩阵（数组）
    """
    # 先定义预测值的数组，大小等于测试样例大小，用0填充
    estimate = np.full(len(df_test), 0, dtype=int)
    # 定义大小为56的全1数组，用于在 X 矩阵前插入一列全 1 的数
    one_matrix = np.full(len(df_test), 1, dtype=int)
    # 将测试集中的前13项作为 矩阵 X 的数
    test_matrix = dataframe_to_matrix(get_not_last_column(df_test))
    # X 第一列插入 一列 1
    test_matrix = np.insert(test_matrix, 0, values=one_matrix, axis=1)
    # print(np.size(test_matrix, 0))
    # X 中每一行同 β进行计算，获得预测的价格
    for i in range(np.size(test_matrix, 0)):
        estimate[i] = np.dot(beta, test_matrix[i])

    # print(estimate)
    return estimate


if __name__ == '__main__':
    path = 'boston_housing_data.csv'
    # 读取csv文件，存入 df
    df_housing_data = read_data(path)
    # 获取训练集
    df_training_data = get_training_data(df_housing_data, 450)
    # 获取测试集
    df_test_data = get_test_data(df_housing_data, 56)
    # 获取训练来的 参数
    beta_matrix = model_calculation(get_not_last_column(df_training_data), get_last_column(df_training_data))
    # 测试集与训练结果参数计算获得 预测价格
    estimate_value_price = get_estimate(beta_matrix, df_test_data)
    # 实际价格
    true_value_price = dataframe_to_matrix(get_last_column(df_test_data))
    # 绘制预测值与真实值图
    # 规定字体，避免乱码
    plt.rcParams['font.sans-serif'] = [u'SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.plot(true_value_price, color="r", label="实际价格")  # 颜色表示
    plt.plot(estimate_value_price, color=(0, 0, 0), label="预测价格")
    plt.xlabel("测试序号")  # x轴命名表示
    plt.ylabel("价格")  # y轴命名表示
    plt.title("实际值与预测值折线图")
    plt.legend()  # 增加图例
    plt.show()  # 显示图片
机器学习
#Python #机器学习
多元线性回归 —— 波士顿房价预测
https://muxiner.github.io/ml-boston-housing/
作者
Muxiner
发布于
2022年4月30日
许可协议